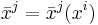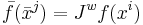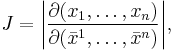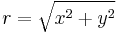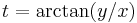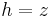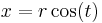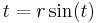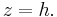Relative scalar
In mathematics, a relative scalar (of weight w) is a scalar-valued function whose transform under a coordinate transform,
on an n-dimensional manifold obeys the following equation
where
that is, the determinant of the Jacobian of the transformation.[1] Relative scalars are an important special case of the more general concept of a relative tensor.
Contents |
Ordinary scalar
An ordinary scalar or absolute scalar[2] refers to the 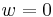 case.
case.
If 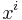 and
and 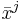 refer to the same point
refer to the same point  on the manifold, then we desire
on the manifold, then we desire 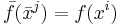 . This equation can be interpreted two ways when
. This equation can be interpreted two ways when 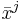 are viewed as the "new coordinates" and
are viewed as the "new coordinates" and 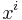 are viewed as the "original coordinates". The first is as
are viewed as the "original coordinates". The first is as 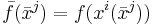 , which "converts the function to the new coordinates". The second is as
, which "converts the function to the new coordinates". The second is as 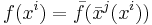 , which "converts back to the original coordinates. Of course, "new" or "original" is a relative concept.
, which "converts back to the original coordinates. Of course, "new" or "original" is a relative concept.
There are many physical quantities that are represented by ordinary scalars, such as temperature and pressure.
Elementary example
Suppose the temperature in a room is given in terms of the function 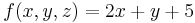 in Cartesian coordinates (x,y,z) and the function in cylindrical coordinates (r,t,h) is desired. The two coordinate systems are related by the following sets of equations:
in Cartesian coordinates (x,y,z) and the function in cylindrical coordinates (r,t,h) is desired. The two coordinate systems are related by the following sets of equations:
and
Using 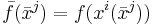 allows one to derive
allows one to derive 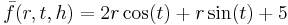 as the transformed function.
as the transformed function.
Consider the point  whose Cartesian coordinates are
whose Cartesian coordinates are  and whose corresponding value in the cylindrical system is
and whose corresponding value in the cylindrical system is 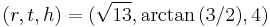 . A quick calculation shows that
. A quick calculation shows that 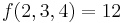 and
and 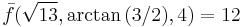 also. This equality would have held for any chosen point P. Thus,
also. This equality would have held for any chosen point P. Thus, 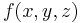 is the "temperature function in the Cartesian coordinate system" and
is the "temperature function in the Cartesian coordinate system" and 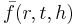 is the "temperature function in the cylindrical coordinate system".
is the "temperature function in the cylindrical coordinate system".
One way to view these functions is as representations of the "parent" function that takes a point of the manifold as an argument and gives the temperature.
The problem could have been reversed. One could have been given 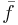 and wished to have derived the Cartesian temperature function
and wished to have derived the Cartesian temperature function  . This just flips the notion of "new" vs the "original" coordinate system.
. This just flips the notion of "new" vs the "original" coordinate system.
Suppose that one wishes to integrate these functions over "the room", which will be denoted by  . (Yes, integrating temperature is strange[says who?] but that's partly what's to be shown.) Suppose the region
. (Yes, integrating temperature is strange[says who?] but that's partly what's to be shown.) Suppose the region  is given in cylindrical coordinates as
is given in cylindrical coordinates as  from
from ![[0,2]](/2012-wikipedia_en_all_nopic_01_2012/I/70fd3f388413505934da60b43afc4088.png) ,
,  from
from ![[0,\pi/2]](/2012-wikipedia_en_all_nopic_01_2012/I/df4639c5677b082cc59d25d1ae0f87e7.png) and
and  from
from ![[0,2]](/2012-wikipedia_en_all_nopic_01_2012/I/70fd3f388413505934da60b43afc4088.png) (that is, the "room" is a quarter slice of a cylinder of radius and height 2). The integral of
(that is, the "room" is a quarter slice of a cylinder of radius and height 2). The integral of  over the region
over the region  is
is
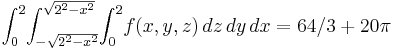 .
.
The value of the integral of 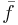 over the same region is
over the same region is
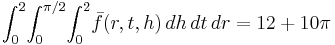 .
.
They are not equal. The integral of an ordinary scalar depends on the coordinate system used. This coordinate dependence tends to remove any physical meaning from the integral of an ordinary scalar.
Scalar density
A scalar density refers to the 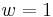 case.
case.
Other cases
Weights other than 0 and 1 do not arise as often. It can be shown the determinant of a type (0,2) tensor is a relative scalar of weight 2.
Generalization
Relative scalars are special cases of relative tensors.
See also
References
- ^ Lovelock, David; Rund (April 1, 1989). "4" (Paperback). Tensors, Differential Forms, and Variational Principles. Dover. p. 103. ISBN 0486658406. http://store.doverpublications.com/0486658406.html. Retrieved 19 April 2011.
- ^ Veblen, Oswald (2004). Invariants of Quadratic Differential Forms. Cambridge University Press. pp. 112. ISBN 0521604842. (page 21)